数学物理方法 Mathematic Method in Physics ¶

约 4655 个字 25 张图片预计阅读时间 16 分钟

Part I : Complex Variable Functions 复变函数 ¶

可导与解析 ¶

复变函数的导数性质 ¶

\[ f'(z) = \lim_{\Delta z \to 0} \frac{f(z+\Delta z)-f(z)}{\Delta z} \]

\(f(z)\) 可导的必要条件：处处满足Cauchy-Reiman Equation

固定另一个为 0，同时对 \(x\) 和 \(y\) 求偏导：

\[ \begin{aligned} f'(z) = f'(x+iy) &= \frac{\partial f}{\partial x} = \frac{\partial u}{\partial x} + i\frac{\partial v}{\partial x}\\ &= \frac 1i \frac{\partial f}{\partial y} = -i\frac{\partial u}{\partial y} + \frac{\partial v}{\partial y} \end{aligned} \]

即有

\[ \boxed{ \begin{cases} \displaystyle{\frac{\partial u}{\partial x} = \frac{\partial v}{\partial y}} \\ \displaystyle{\frac{\partial u}{\partial y} =-\frac{\partial v}{\partial x}} \end{cases} } \]

解析：复变函数 在某一区域内可导，而不能是在某一点或某一线上可导。

Cauchy-Reiman Equation

计算 \(|z|\) 是否可导 / 解析？

\(|z| = \sqrt{x^2+y^2}\)，所以 \(u=\sqrt{x^2+y^2}\)，\(v = 0\)，计算偏导数得到：

\[ \begin{gathered} \frac{\partial u}{\partial x} = \frac{x}{\sqrt{x^2+y^2}}, \frac{\partial u}{\partial y} = \frac{y}{\sqrt{x^2+y^2}}, \quad \frac{\partial v}{\partial x} = \frac{\partial v}{\partial y} = 0 \end{gathered} \]

可见 \(\begin{cases} \displaystyle{\frac{\partial u}{\partial x} = \frac{\partial v}{\partial y}} \\ \displaystyle{\frac{\partial u}{\partial y} =-\frac{\partial v}{\partial x}} \end{cases}\)不能同时满足，故不解析。

计算 \(u(x,y)\) 的二阶微分有：

\[ \begin{aligned} \nabla^2u &= \frac{\partial^2u}{\partial x^2}+ \frac{\partial^2u}{\partial y^2}\\ &= \frac{\partial}{\partial x}\frac{\partial v}{\partial y} + \frac{\partial}{\partial y}(-\frac{\partial v}{\partial x})\\ &= 0 \end{aligned} \]

同理有：

\[ \nabla^2v = 0 \]

这被称为 ( 共轭 ) 调和函数 ，其充分条件是满足 Cauchy-Reiman 方程。

同理还可证：

\[ \nabla^2(uv) = 0 \]

Note

很多情况下 \(u(x,y)\) 和 \(v(x,y)\) 均为初等函数，根据二阶导有：

\[ \frac{\partial^2u}{\partial x^2} = \frac{\partial^2u}{\partial y^2} = \frac{\partial^2u}{\partial (xy)} = 0 \]

通过积分求解解析函数 ¶

我们知道

\[ dv = \frac{\partial v}{\partial x}dx + \frac{\partial v}{\partial y}dy = -\frac{\partial u}{\partial y}dx + \frac{\partial u}{\partial x}dy \]

因此，只要知道任一解析函数的实部 \(u(x,y)\) 或虚部 \(v(x,y)\)，即可求出其另外一个部分

Eg1

\(f(z)\) 解析且 \(\mathrm{Re} f = u(x,y) = 2xy\), 求 \(f(z)\)

观察有 \(dv = -2xdx + 2ydy = d(y^2-x^2)\)，于是 \(v = y^2-x^2+C\)

\[ f(z) = 2xy + i(y^2-x^2+C) = -i(x+iy)^2 + iC = -iz^2+iC \]

采取共轭复数的求解（不积分）¶

\[ \begin{cases} x = \displaystyle{\frac{z+z^*}{2}}\\ y = \displaystyle{\frac{z-z^*}{2i}} \end{cases} \]

于是

\[ \frac{\partial f}{\partial z^*} = \frac{\partial f}{\partial x}\frac{\partial x}{\partial z^*} + \frac{\partial f}{\partial y}\frac{\partial y}{\partial z^*} = \frac 12 \frac{\partial f}{\partial x} - \frac{1}{2i}\frac{\partial f}{\partial y} = 0 \]

这意味着 \(f\) 与 \(z^*\) 无关。又有

\[ \begin{aligned} f(x+iy) &= u(x, y)+iv(x, y)\\ f^*(x-iy) &= u(x, y)-iv(x, y) \end{aligned} \]

若已知实部，我们有：

\[ u(x, y) = \frac{f(x+iy)+f^*(x-iy)}{2} \]

若令：\(x+iy = z, x-iy = 0\)，则 \(x=\frac z2,y = \frac{z}{2i}\)

\[ \begin{aligned} f(z) &= 2u(\frac z2,\frac{z}{2i}) -f^*(0) \\ &= 2u(\frac z2,\frac{z}{2i}) - u(0,0) + iv(0,0)\\ &= 2u(\frac z2,\frac{z}{2i}) - u(0,0) + iC \end{aligned} \]

Note

若函数在 0 处无定义，可取解析域内 \(x-iy = z_0\)。eg：\(u = \frac{x}{x^2+y^2}\)

Warning

此处的 \(z\) 和 \(z^*\) 为“形式化推导”的产物，即两者并不存在数量关系（不一定同时等于 0）

特殊情况下的处理 ¶

Eg2

\(f(z)\) 解析且已知 \(u+v\)，求 \(f(z) = u+iv\)

设

\[ F = u+v+\mathrm{Im}(F) = u+v + iv-iu = (1-i)f \]

此时退化成 \(U(x,y) = u+v\) 已知的解析函数求解。

Eg3

\(f(z)\) 解析且已知 \(uv\)，求 \(f(z) = u+iv\)

求平方有：

\[ f^2 = u^2 - v^2 + i(2uv) = U(x, y) + iV(x, y) \]

此时退化成 \(V(x,y) = 2uv\) 已知的解析函数求解。

初等函数 ¶

幂函数 ¶

\[ f(z) = z^n,\quad n\in\mathbb{C} \]

for \(n = 1,2,3 ...\), \(f(z)\) 在 \(\infty\) 不解析，但在 \(\mathbb{C}\) 解析

for \(n = -1,-2,-3 ...\), \(f(z)\) 在 \(\mathbb{C}/0\) 上解析

指数函数 ¶

\[ f(z) = e^z \]

表现为周期函数且 \(e^x>0\quad if\quad x\in\mathbb{R}\)

\(e^z+1=0\) 在 \(\mathbb{R}\) 内无解但在 \(\mathbb{C}\) 内有无穷多解，since \(e^{i\pi + 2k\pi} = -1\)

于是其解 \(z = i\pi + 2k\pi\)

实部图像	虚部图像

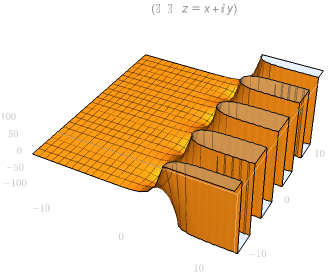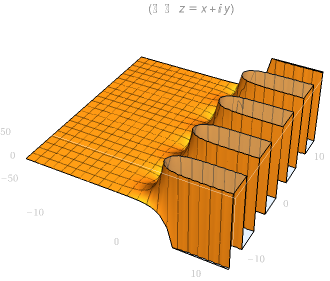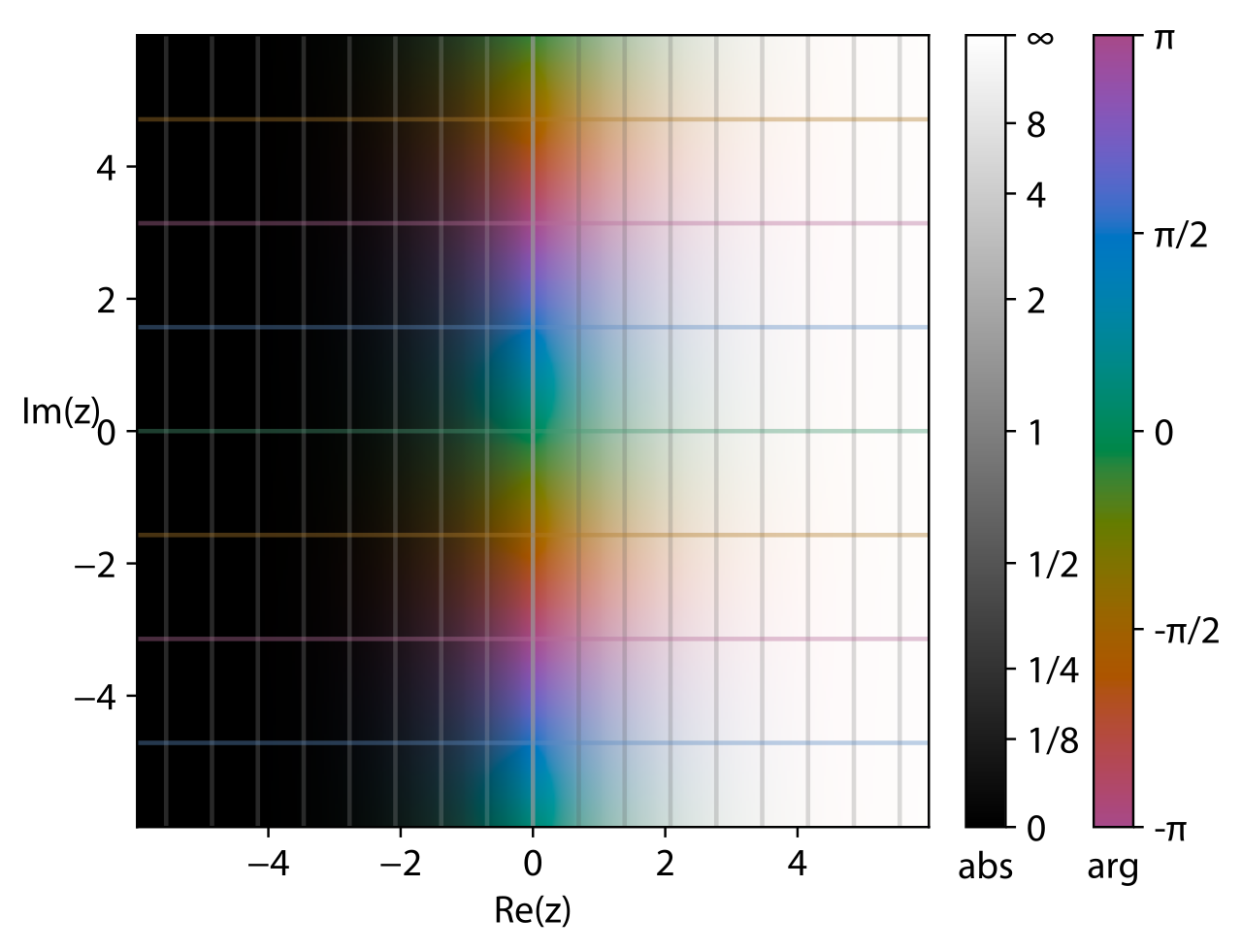
三角函数 ¶

\[ f(z) = \sin z, \cos z, \tan z, \cot z \]

对于复数域可能有 \(|\sin z| > 1\)

由欧拉公式我们有：

\[ \begin{aligned} \sin z &= \frac{e^{iz} - e^{-iz}}{2i} \\ \cos z &= \frac{e^{iz} + e^{-iz}}{2} \end{aligned} \]

sin(z) 实部图像	sin(z) 虚部图像

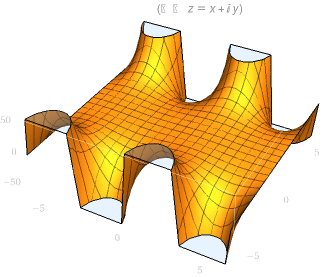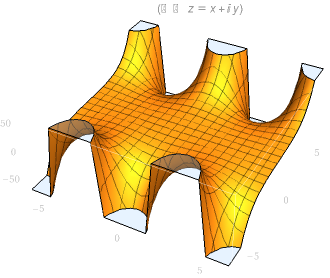cos(z) 实部图像	cos(z) 虚部图像

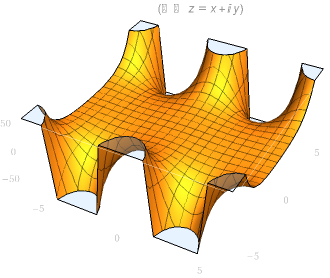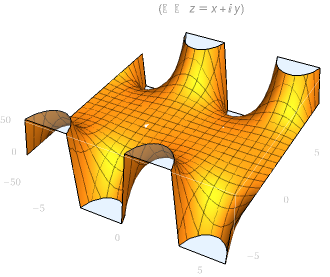双曲函数形式：

\[ \begin{aligned} \sinh z &= \frac{e^z - e^{-z}}{2} \\ \cosh z &= \frac{e^z + e^{-z}}{2} \end{aligned} \]

若要讨论函数在无穷远点的性质，取变量替换 \(t = \frac 1z\)

本性奇点：既非极点，也不可去。eg：

\[ e^{1/z} \quad \text{for} \quad z = 0 \]

多值函数 ¶

根式函数的多值性 ¶

讨论函数：

\[ \begin{aligned} w &= \sqrt{z-a}\\ w^2 &= z-a \end{aligned} \]

若令 \(w = \rho e^{i\phi}\), \(z-a = r e^{i\theta}\)

\[ \rho^2 e^{i2\phi} = re^{i\theta} \]

于是

\[ \begin{cases} r = \sqrt{\rho}\\ \theta = 2\phi + 2k\pi \end{cases} \]

即为 \(\mathrm{arg}(\sqrt{z-a}) = \frac 12 \mathrm{arg}(z-a)\)，这意味着对于函数 \(w\)，如果考虑 \(z\) 在 \(a\) 点附近旋转一圈，在 \(w\) 平面上只旋转了半圈。

\(\sqrt{z}\) 的图像如下图所示，可见虚部是螺旋上升的：

实部图像	虚部图像

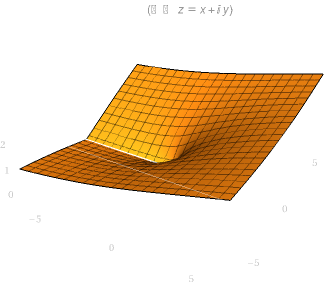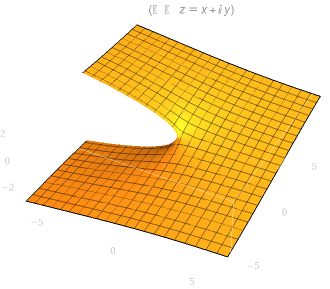这种单一自变量对应多个函数值的函数被称为 多值函数

多值函数的单值化 ¶

考虑模和辐角：

\[ \begin{gathered} |w| = \sqrt{|z-a|} \\ \arg{w} = \frac 12\arg(z-a) \end{gathered} \]

可见其多值性 体现在辐角而不是模上（相差 \(\pi\) 而不是 \(2\pi\)）

\[ \frac 12 (\arg(z-a)+2\pi) = \arg w+\pi \]

多值性的根源：宗量（作为自变量的函数）\(z-a\) 具有任意性

简单的办法是限制其辐角变化范围（\(\arg(z-a) \in [0,2\pi)\)），即在平面上作割线，此时 \(\arg w \in [0,\pi)\)，意味着 \(w\) 只位于平面上半部分，这被称为一个 单值分支

此处割线的作用是限制辐角的变化方式，规定 割线上岸 为 \(\arg(z-a)=0\)

同理，如果限制 \(\arg(z-a) \in [2\pi, 4\pi)\)，有 \(\arg w \in [\pi,2\pi)\)，这是 \(\sqrt{z-a}\) 的另一个单值分支：

单值分支 I	单值分支 II

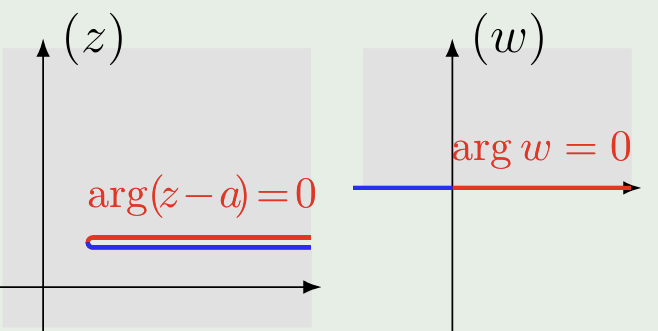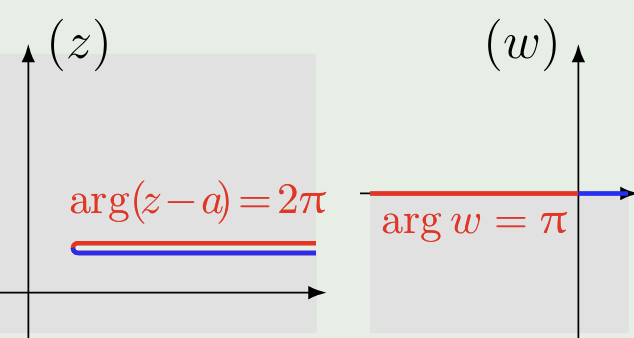据此可以判断这一类函数的多值性。

判断函数的多值性

判断以下函数是否为多值函数

\[ (1)\sin \sqrt{x}, (2)\cos \sqrt{x}, (3)\frac{\sin \sqrt{x}}{\sqrt {x}}, (4)\frac{\cos \sqrt{x}}{\sqrt {x}} \]

由根式函数的两个分支互为相反数，可注意到：

\[ \cos (-w) = \cos(w), \frac{\sin (-w)}{-w} = \frac{\sin (w)}{w} \]

即 (2)(3) 中两个分支中，每一对相反数函数值均相同，可视为一个单值分支。于是 (2)(3) 为单值函数。

分支点 ¶

在上面的讨论中，考虑函数 \(w=\sqrt{z-a}\)，自变量 \(z\) 绕点 \(a\) 旋转两圈（同时也是绕无穷远点 \(\infty\) 旋转）其函数值才能复原，因此我们可以说 \(z=a\) 和 \(z=\infty\) 是函数 \(w=\sqrt{z-a}\) 的 分支点，其 分支指数 为 2。

小贴士

想象分支点连着一根线到路径上，让这个绳子缠在分支点上几圈就是绕这个点转的辐角。

讨论函数：

\[ w = \sqrt [4]{(z-a)(z-b)} \]

我们写成辐角形式：

\[ \begin{aligned} w^4 &= r_1r_2e^{i(\theta_1+\theta_2)}\\ 4\arg w &= \theta_1 + \theta_2 \end{aligned} \]

可以看，当 \(z\) 绕 \(z=a\) 和 \(z=b\) 四圈才能让函数值复原，因此其分支指数为 4；而同时绕两个点（\(即绕z=\infty\)）两次即可复原，分支指数为 2。

要想让其为单值函数，必须做割线使得 \(z\) 不能绕任意一个分支点一圈，因此通常我们分别做连接 \(z=a\) 和 \(z=\infty\) 的射线和连接 \(z=b\) 和 \(z=\infty\) 的射线。

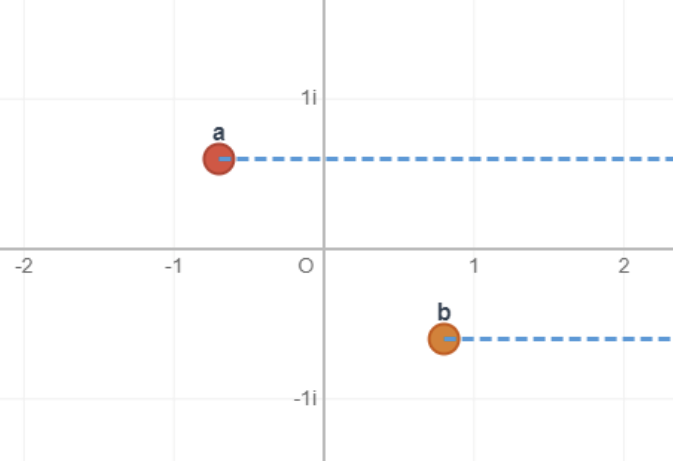
Reimann 面 ¶

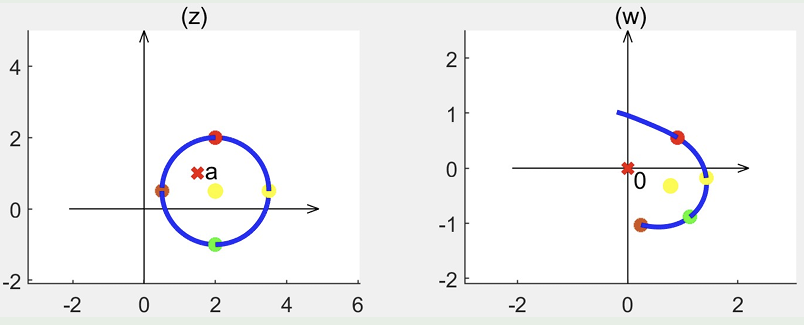
另一种方法是，规定复变函数在某一点的值，描述其 沿某一路径 运动到另一点的值。

先考虑函数 \(w = \sqrt{1-z}\)，规定 \(w(2) = -i\)，考虑 \(C_1\) 和 \(C_2\) 两种路径：

路径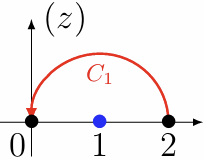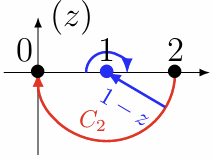
\(\Delta \arg(1-z)\)	\(\pi\)	\(-\pi\)
\(\arg(1-z)\)	\((4k-1)\pi + \pi = 4k\pi\)	\((4k-1)\pi - \pi = (4k-2)\pi\)
\(w\)	\(e^{\frac{4k\pi}{2}i} = 1\)	\(e^{\frac{(4k-2)\pi}{2}i} = -1\)

在几何图形上，我们可以视作两个平面粘合起来（其实这个图形不能用三维描述）：

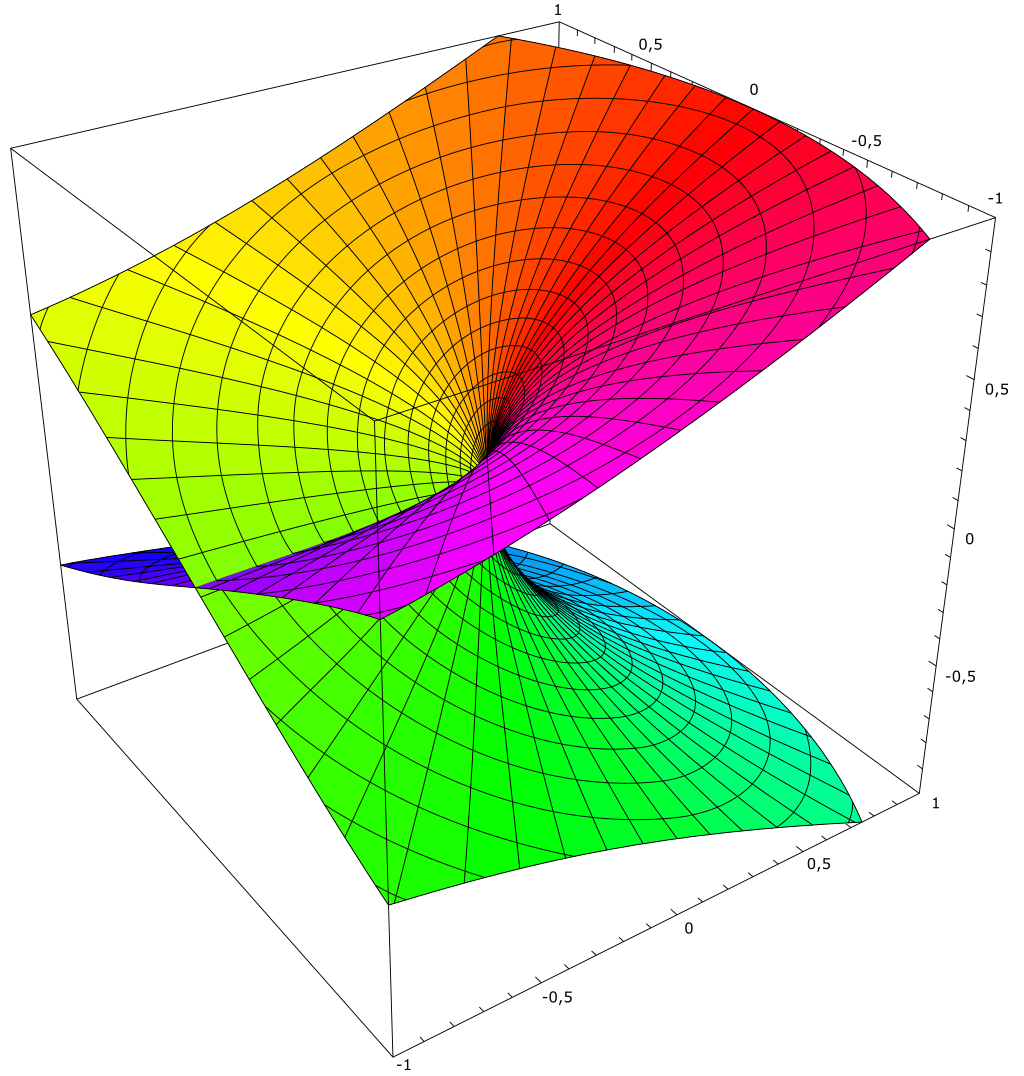
可以看到对于任意点绕原点的运动，只有在这个诡异的平面上转两圈才能复原；这种曲面就是 Reiman 面，对于这种根式函数有 二叶 Reiman 面。

对数函数 ¶

考虑复平面的对数函数：

\[ w = \ln(z) \]

令 \(w = u+iv\), \(z = re^{i\theta}\)，我们有：

\[ \begin{gathered} u = \ln r = \ln \abs{z}, v = \theta + 2n\pi \\ w = \ln \abs{z} + i(\arg{z} + 2n\pi) \end{gathered} \]

也就是其每一个 \(z\) 空间内的点对应 \(w\) 空间实部相同的无数点：

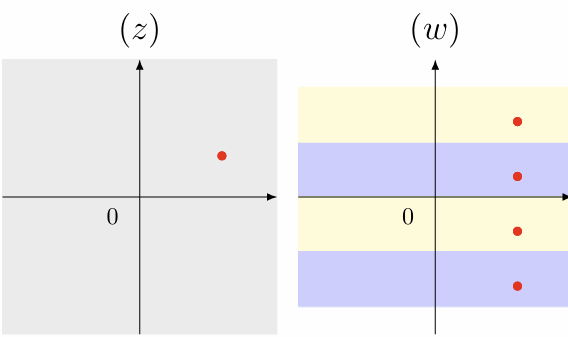
其限制在 \([-\pi,\pi)\) 内的函数图像：

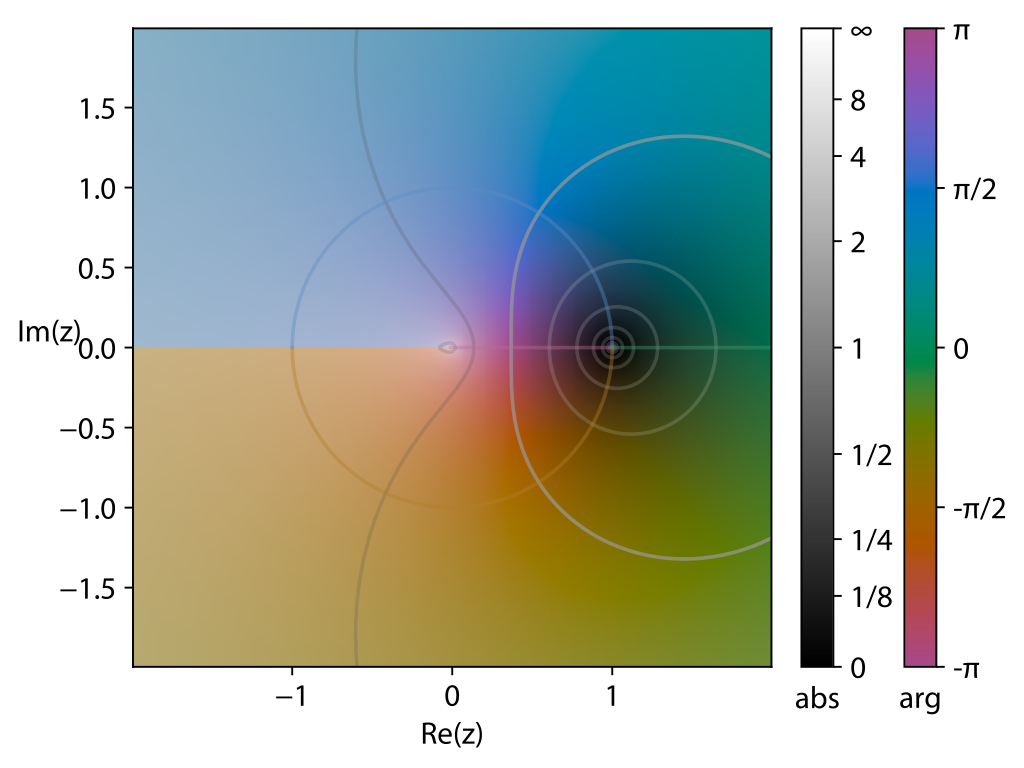
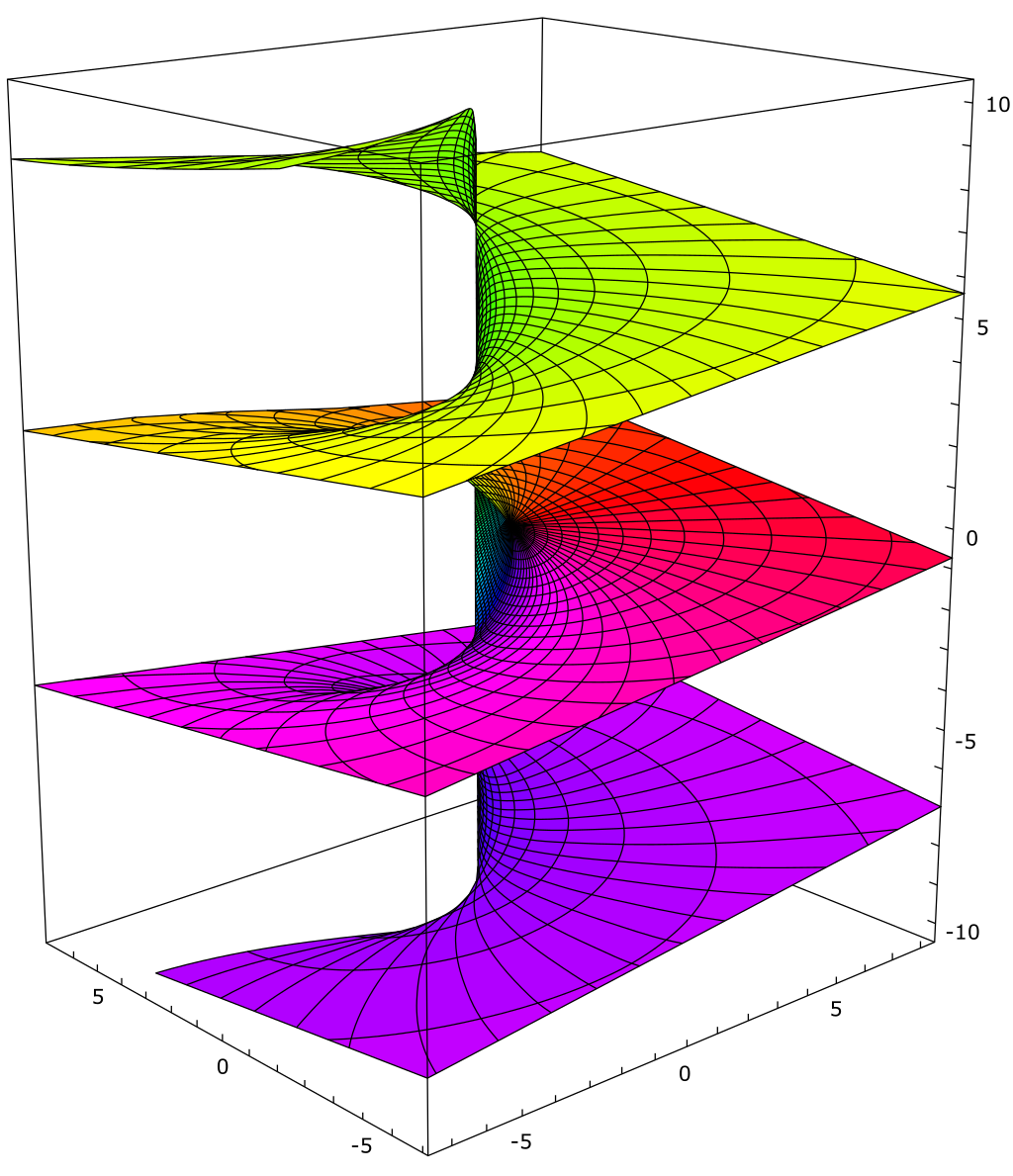
显而易见其分支点是 \(z=0\) 和 \(z=\infty\)，于是做原点出发的射线可以使对数函数 \(\ln z\) 单值化。其 Reiman 面是无穷叶的：

反三角函数 ¶

\[ \begin{aligned} \arcsin z &= \frac 1i \ln(iz+\sqrt{1-z^2})\\ \arccos z &= \frac 1i \ln(z+\sqrt{z^2-1})\\ \arctan z &= \frac 1{2i} \ln(\frac{1+iz}{1-iz}) \end{aligned} \]

复变积分 ¶

复变积分的定义 ¶

复变积分就是 复平面上的第一类曲线积分

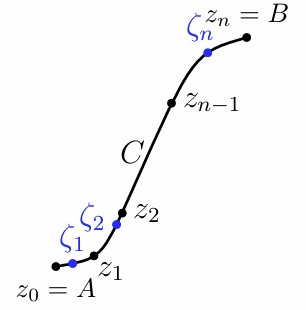
\[ \begin{aligned} \int_C f(z)dz &= \lim_{\abs{z_k-z_{k-1}}\to 0} \sum_{k = 1}^n f(\zeta_k)(z_k - z_{k-1}) \\ \end{aligned} \]

其可以拆成两个线积分的组合：

\[ \begin{aligned} \int_C f(z)dz &= \int_C(u+iv)(dx+idy) \\ &= \int_C(udx-vdy) + i\int_C(vdx+udy) \end{aligned} \]

于是如果 \(C\) 可求长，而 \(f(z)\) 在 \(C\) 上连续，则复变积分 \(\int_C f(z)dz\) 一定存在。

复变积分的直接求法

要求：

\[ \int_C z^ndz \]

已知 \(n\) 为整数，\(C\) 为以原点为原型，\(r\) 为半径，夹角为 \(\theta_2-\theta_1\) 的圆弧。

可以得出：

\[ \begin{aligned} \int_C z^ndz &= \int_C r^n e^{in\theta}d(re^{i\theta}) \\ &= ir^{n+1} \int_C e^{in\theta}·e^{i\theta} d\theta \\ &= ir^{n+1} \int_C e^{i(n+1)\theta} d\theta \end{aligned} \]

此处需要分类讨论。当 \(n=-1\) 时我们有：

\[ \int_C z^ndz = i(\theta_2 - \theta_1) \]

在其他情况下：

\[ \begin{aligned} \int_C z^ndz &= ir^{n+1} \int_C e^{i(n+1)\theta} d\theta \\ &= ir^{n+1} (\frac{e^{i(n+1)\theta_2} - e^{i(n+1)\theta_1}}{i(n+1)}) \\ &= \frac{r^{n+1}}{n+1} (e^{i(n+1)\theta_2} - e^{i(n+1)\theta_1}) \end{aligned} \]

注意：如果对复数微元取模（即取弧长微元）：

\[ \abs{dz} = ds = \sqrt{r'(\theta)^2 + r^2}d\theta = rd\theta = \sqrt{1+(y')^2}dx \]

则有

\[ \int_C z^n\abs{dz} = r^{n+1} \int_C e^{in\theta} d\theta = \begin{cases} r(\theta_2 - \theta_1),& n = 0 \\ \displaystyle r^{n+1}\cdot\frac{e^{in\theta_2} - e^{in\theta_1}}{in},& n\neq0 \end{cases} \]

复变积分的分解求法

求 \(\int_C zdz\), \(C\) 为直线 \(0 \to 1+i\)

\[ \begin{aligned} \int_C zdz &= \int_C(x+iy)d(dx + idy) \\ &= \int_C (xdx-ydy) + i\int_C (ydx + xdy) \\ &= \frac12 - \frac12 + i = i \end{aligned} \]

事实上，这个积分是一个整函数，可以直接有：

\[ \int_C zdz = \frac 12 z^2 \big|_0^{1+i} = i \]

复变积分的 所有基本性质与曲线积分类似。

Cauchy 定理与不定积分 ¶

如果函数 \(f(z)\) 满足：

在有界单连通区域 \(G\) 内解析；
积分路径 \(C\) 为 \(G\) 内任意一条首尾相接的可求长曲线；

则有：

\[ \boxed{\oint f(z)dz = 0} \]

这被称为 Cauchy 积分定理。

注意

单连通区域只能是有界区域，不能是绕 \(\infty\) 的无界区域。例如 \(f(z) = \frac 1z\) 沿 \(\infty\) 一周的积分不为 0（即使是解析的）。由于在 \(G\) 内解析，曲线 \(C\) 不可包含任何无定义或不可导点。

推论

若 \(f(z)\) 在有界单连通区域 \(G\) 内解析，则对任意 \(C \subset G\) 有：

\[ \int_C f(z)dz \quad \text{与路径无关} \]

Question

Cauchy 定理和 Cauchy-Reiman 方程互为微分 / 积分形式。

这也提供了 Cauchy 定理的证明：由 Green 公式：

\[ \begin{aligned} \oint_C f(z)dz &= \int_C(udx-vdy) + i\int_C(udy + vdx) \\ &= \iint_D (- \frac {\partial v}{\partial x} - \frac {\partial u}{\partial y}) +i \iint_D (\frac {\partial u}{\partial x} - \frac {\partial v}{\partial y}) \end{aligned} \]

然后应用 Cauchy-Reiman 方程：

\[ \frac {\partial v}{\partial x} = - \frac {\partial u}{\partial y}, \quad \frac {\partial v}{\partial y} = \frac {\partial u}{\partial x} \]

可知：

\[ \oint_C f(z)dz = 0 \]

事实上，格林公式的应用条件是导函数存在且连续，而在一般的解析函数并未定义导函数连续。但由 Goursat 定理可证：解析函数的任意阶导函数存在且连续（即无限可微）。证明懒得写。

由 Cauchy 定理推论，可以知道在有界单连通区域 \(G\) 内的函数：

\[ \boxed{\int_{z_0}^z f(\zeta)d\zeta = F(z)} \]

为单值函数。这也被称作 \(f(z)\) 的 不定积分。我们有：

\[ F'(z) = \frac{d}{dz}\int_{z_0}^z f(\zeta)d\zeta = f(z) \]

\(f(z)\) 被称为 \(F(z)\) 的 原函数。（并不唯一，可以相差常数 C）

\[ F(z) = \Phi(z) +C \]

显然有：

\[ \begin{aligned} F(z_0) = \Phi(z_0) + C &= 0 \\ C &= -\Phi(z_0) \\ F(z) = \int_{z_0}^z f(\zeta)d\zeta = \Phi(z) +C &= \Phi(z) - \Phi(z_0) \end{aligned} \]

注意

引用以上公式的时候必须首先说明 \(f(z)\) 在某一单连通区域内解析。

多连通区域 ¶

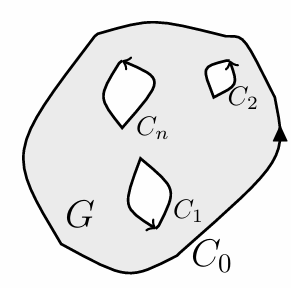
对于多连通区域，我们有：

\[ \boxed{\oint_{C_0} f(z)dz = \sum_{n} \oint_{C_i}f(z)dz} \]

其中 \(C_0\) 为外部框线的环路积分，\(C_i\) 为内部框线的环路积分。注意对于这里的内部框线，指的是将内部的洞视为一个“区域”时这个区域的边界，因此积分方向是逆时针，有别于一般内部框线的定义。

证明可以通过构造下列割线形成单连通区域 \(G'\)：

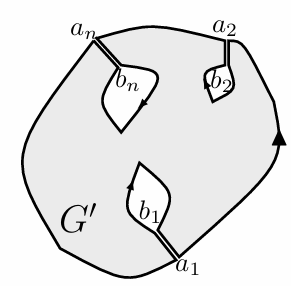
由于割线两岸积分相互抵消，整个 \(G'\) 的环路积分为 0，移项可以得到结果。

\[ \oint_{C_0} f(z)dz - \sum_{n} \oint_{C_i}f(z)dz + \sum_n \int_{a_i}^{b_i} f(z)dz + \sum_n \int_{b_i}^{a_i} f(z)dz = 0 \]

求环路积分

计算 \(\oint_C z^ndz\)，其中 \(n \in \mathbb{R}\)

显然当 \(n \in \mathbb{N}\)（\(\mathbb{C}/\infty\) 内解析）和 \(C\) 内不含 \(z=0\) 时，有

\[ \oint_C z^ndz = 0 \]

而当 \(n\) 为负整数且 \(C\) 内含有原点时：

\[ \begin{aligned} \oint_C z^ndz &= \int_{\abs{z} = \epsilon} z^ndz = i\epsilon^{n+1}\int_0^{2\pi} e^{in\theta} \cdot e^{i\theta} d\theta \\ &= i\epsilon^{n+1}\int_0^{2\pi} e^{i(n+1)\theta} d\theta = \begin{cases} 2\pi i, &n =-1 \\ 0, &n = -2,-3,-4, ... \end{cases} \end{aligned} \]

在未给定圆形路径的半径 \(r\) 或比较难算时，常常采用在奇点附近取 \(|z-a|\to0\) 的小圆，通过极限求得其路径积分。

大小圆弧引理 /Jordan 引理 ¶

一致收敛

逐点收敛：当 \(z\to a\) 时，\(f(z,w) \to A\)，iff：

\[ \forall \epsilon > 0, \exists \delta(w)> 0, s.t. 当\abs{z-a}<\delta 时，\abs{f(z, w)-A}<\epsilon \]

一致收敛：当 \(z\to a\) 时，\(f(z,w) \rightrightarrows A\)，iff：

\[ \forall \epsilon > 0, \exists \delta > 0, s.t. 对\forall w\in G, 当\abs{z-a}<\delta 时，\abs{f(z, w)-A}<\epsilon \]

注意此时 \(\delta\) 和 \(w\) 无关，也可以理解为 \(\sup{f(z,w)} \to 0\)。

作为例子，当 \(f(z,w)=zw\) 时，考虑 \(z\to0\)：

\[ \forall \epsilon > 0, \exists \delta(w) = \frac{\epsilon}{|w|}> 0, s.t. \abs{f(z, w)-0} = \abs{zw}<\epsilon \]

因此 \(f(z,w) \to 0\)。

考虑有限区域 \(G= \{z,|z|<M\}\)，考虑 \(z\to0\)：

\[ \forall \epsilon > 0, \exists \delta = \frac{\epsilon}{M}> 0, s.t. \abs{f(z, w)-0} = \abs{zw}<|\frac {\epsilon w} M| \le \epsilon \]

因此 \(f(z,w) \rightrightarrows 0\)。但是，如果考虑无限区域，则找不到 \(\delta\)，因此不是一致收敛。这意味着一致收敛比逐点收敛的条件更强。

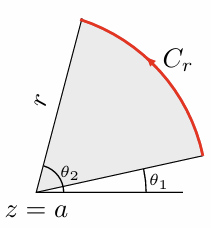
小圆弧引理：\(f(z)\) 在灰色区域内连续，令 \(z-a=re^{i\theta}\)，且有 扇形区域内 一致收敛：

\[ (z-a)f(z) = re^{i\theta}f(a+re^{i\theta}) \rightrightarrows k \]

则：

\[ \lim_{r\to0} \int_{C_r} f(z)dz = ik(\theta_2-\theta_1) \]

注意

只是扇形区域内一致收敛，而不是极限是 \(k\)。后者的条件更强（包括了所有辐角）。

eg：当 \(z\to0\) 时，\(\displaystyle f(z)=e^{\frac 1z} = \exp(\frac 1r e^{-i\theta})\) 的极限不存在，但存在扇区内一致收敛。

考虑 \(\displaystyle \frac{\pi}{2} < \frac \pi2+\xi < \theta < \pi\) 范围内，显然 \(f(r,\theta) \rightrightarrows 0\)。

化简原式：

\[ \abs{\exp(\frac 1r e^{-i\theta})} = \abs{\exp(\frac1r(\cos\theta-i\sin\theta))} = e^{\frac{\cos\theta}{r}} < e^{\frac{\cos(\frac\pi2 + \theta)}{r}} = e^{\frac{-\sin\theta}{r}} < \epsilon \]

于是我们可以说：

\[ \forall \epsilon > 0, \exists \delta = -\frac{\sin\epsilon}{\ln\epsilon}, s.t. 当 r <\delta 时，f(r,\theta)<\epsilon \]

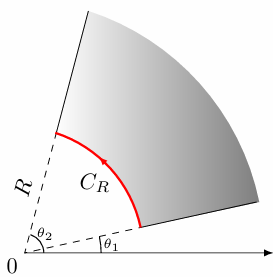
大圆弧引理：\(f(z)\) 在灰色区域内连续，令 \(z=re^{i\theta}\)，且有 扇形区域内 一致收敛：

\[ zf(z) = Re^{i\theta}f(Re^{i\theta}) \rightrightarrows K \]

则：

\[ \lim_{R\to\infty} \int_{C_R} f(z)dz = iK(\theta_2-\theta_1) \]

含参定积分 ¶

Cauchy 积分公式 ¶

如果函数 \(f(z)\) 满足：

在有界区域 \(G\) 内解析，闭区域 \(\overline{G}\) 内连续且边界 \(\partial G\) 可求长；
\(a \in G\)

就有：

\[ f(a) = \frac 1{2\pi i} \oint_{\partial G} \frac{f(z)}{z-a}dz \]

这被称为 有界区域的 Cauchy 积分公式

在特殊情况下，常用圆周型区域 \(d(z-a) = iRe^{i\theta}d\theta\)，有

\[ f(a) = \frac 1{2\pi} \int_0^{2\pi}f(a+Re^i\theta) d\theta \]

这就说明 \(f(a)\) 等于在解析区域内，以 \(a\) 为圆心的圆周上的积分值的平均值（均值定理）。

证明

在 \(z-a\) 附近取圆周 \(\abs{z-a} = r\)，由多连通区域的 Cauchy 定理：

\[ \oint_{\partial G} \frac{f(z)}{z-a}=\oint_{\abs{z-a} = r} \frac{f(z)}{z-a} \]

在 \([0,2\pi)\) 内使用小圆弧定理：

\[ \lim_{r\to0} \oint_{\abs{z-a} = r} \frac{f(z)}{z-a} = 2\pi i \cdot \lim_{(z-a) \to 0} (z-a)\frac{f(z)}{z-a} = 2\pi i f(a) \]

如果拓展到无解区域内，函数 \(f(z)\) 满足：

在无界区域 \(G\) 内单值解析，闭区域 \(\overline{G}\) 内连续且边界 \(\partial G\) 可求长；
\(a \in G\)；
\(\lim_{z\to\infty}f(z) = 0\) 且存在一个原点为圆心的大圆 \(C_R\)，使得大圆外的区域均解析

就有：

\[ f(a) = \frac 1{2\pi i} \oint_{\partial G} \frac{f(z)}{z-a}dz \]

证明

取一个足够大的大圆 \(\abs{z} = R\)，对有界区域有：

\[ f(a) = \frac{1}{2\pi i}\oint_{\partial G} \frac{f(z)}{z-a}dz + \frac{1}{2\pi i}\oint_{C_R} \frac{f(z)}{z-a}dz \]

取 \(R\to\infty\)，由大圆弧引理：

\[ f(a) = \frac{1}{2\pi i}\oint_{\partial G} \frac{f(z)}{z-a}dz + \lim_{z\to\infty}f(z) = \frac{1}{2\pi i}\oint_{\partial G} \frac{f(z)}{z-a}dz \]

求 Cauchy 型积分

一定注意该公式使用的前提是 \(f(z)\) 在区域 \(G\) 内解析！如果需要积分 \(\frac{\phi(z)}{(z-a)(z-b)}\)：

如果 \(a \in G\)，而 \(b \notin G\)，可以将 \(a\) 作为外部的 \((z-a)\) 项（避免奇点在区域内部）。
如果 \(a \in G\)，且 \(b \in G\)，可考虑分式分解成 \(\frac{A}{z-a} + \frac{B}{z-b}\)。

Cauchy 型积分 ¶

若 \(C \subset \mathbb{C}\) 是一条可求长曲线，定义 Cauchy 型积分：

\[ F_n(z) = \int_C \frac{\varphi(\zeta)}{(z-\zeta)^n} d\zeta,\quad z\notin C, \quad n\in\mathbb{N} \]

有如下性质：

\(F_n(z)\) 对任意 \(z \notin C\) 均解析；
\(F_{n}'(z) = nF_{n+1}(z)\)

Cauchy 积分公式的右侧实际上可看作 Cauchy 型积分的 \(n=1\) 形式。

观察性质 2，其实有：

\[ \begin{aligned} F_n'(z) = \frac{d}{dz} \int_C \frac{\varphi(\zeta)}{(z-\zeta)^n} d\zeta &= n\int_C \frac{\varphi(\zeta)}{(z-\zeta)^{n+1}} \\ &= \int_C \frac{d}{dz} \frac{\varphi(z)}{(z-\zeta)^{n+1}} \end{aligned} \]

即对于 Cauchy 型积分 微商和积分可互换。

由此性质可以推出 高阶导数公式（有界区域及无界区域的要求同 Cauchy 积分）：

\[ f^{(n)}(z) = \frac{n!}{2\pi i}\oint_{\partial G} \frac{f(\zeta)}{(z-\zeta)^{n+1}} d\zeta \]

这意味着对于一个解析函数，只要一阶导数存在，则任意阶导数均存在。

含参变量积分 ¶

对于含参复变函数 \(f(t,z)\)，若满足：

对于 \(t \in [a,b]\)， \(z \in \overline{G}\)，\(f(t,z)\) 对 \(t\) 和 \(z\) 均连续；
\(\forall t\in [a,b]\)，\(f(t,z)\) 在 \(G\) 内解析且在 \(\overline{G}\) 中连续；

则有：

函数 \(F(z) = \int_a^b f(t,z)dt\) 在 \(G\) 内解析；
\(f(z)\) 积分号和微商号可互换，即：

\[ \frac{d}{dz} \int_a^b f(t, z) dt = \int_a^b [\frac{\partial}{\partial z}f(t, z)] dt \]

无穷级数 ¶

无穷级数的判别方法大致与 3